From
tabletop roleplaying games, to simple random draw needs, I've
always felt the specific requirement of a higher than six-faced die a
bit limiting, especially when the easiest dice sets to find around
are often pairs of regular six-faced dice.
So, how can we make use of every possible combination of a two
six-faced dice
roll and get bigger-than-12 results?
Here's
the
most viable solution I came up with:
to
obtain up to 36 unique results from a two
six-faced dice roll, one of the dice keeps its faces as is, while the
second die has its faces replaced by new values (through stickers
and/or
markers).
This
is the generic rule to follow when assigning the "expansion
values" to each face (no matter the
face-configuration chirality
of the die):
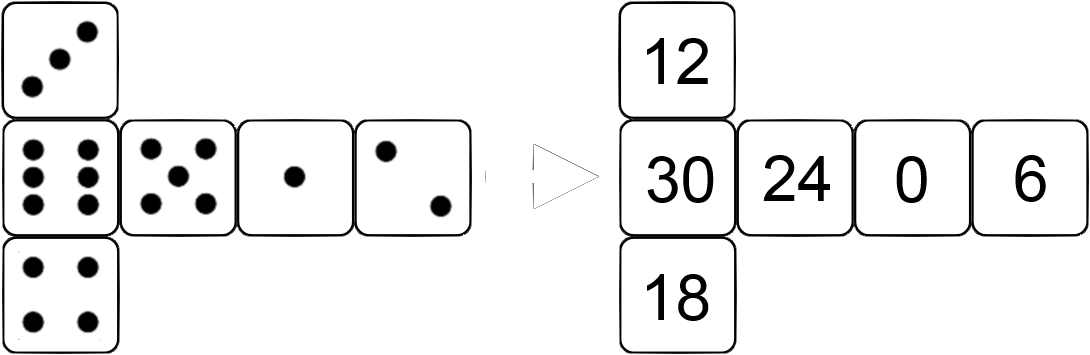
These
positions preserve a constant top-bottom sum of 30, just like the
constant top-bottom sum of 7 on a regular six-faced die.
After
a roll of both dice, the sum of the value on the expansion die's
top face and the value of the regular one's will always provide a
result between 1 and 36.
I've
personally tried it with square pieces of white masking
tape and the use of a permanent marker to write the expansion values.
If well cut and neatly applied, the duct tape's effect on
the roll's fairness is negligible.
In
any case, this kind of solution is probably
the only one able to overcome "emergency" situations where a +6
polyhedral die isn't readily available.
This
is what the pair of dice looked like in my test:
So,
to recap, the main advantages of this system are:
- A single roll of the expanded pair of six-faced
dice can return up to the highest result of 3 summed rolls of a pair of
regular six-faced dice [max result possible (12) times rolls (3) = 36];
- Presence of number 1 (when the hand-numbered die
is equal to 0 and the regular one to 1);
- No repeating outcomes, so the probability of
getting some results more often than others is none (uniform
distribution instead of normal, basically behaving like a single
tricontahexahedral die).


